3.1.4 Propiedades de la igualdad
La igualdad relaciona dos expresiones con el signo “=”, la igualdad tiene algunas propiedades que son verdades evidentes, no requieren ser demostradas, a partir de estas propiedades se pueden demostrar otras propiedades. Las primeras cuatro propiedades que se muestran a continuación son propiedades evidentes de la igualdad:
Considera que a, b, c 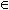 R R
Propiedad |
Proposición |
Ejemplo |
Propiedad reflexiva:
Todo número es igual a si mismo |
a = a
|
5 = 5 |
Propiedad de simetría:
Si un número es igual a otro, éste es igual al primer |
Si a = b 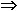 b = a b = a
|
x = 4 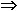 4 = x 4 = x |
Propiedad transitiva:
Si un número es igual a un segundo número y éste es igual a un tercero, el primero y el tercero son iguales |
Si a = b y b = c 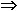 a = c a = c |
x = 4 y 4 = z 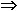 x = z x = z |
Propiedad de sustitución:
Si un número es igual a otro, en cualquier expresión en que aparezca el primero puede reemplazarse por el segundo |
Si a = b 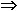 a puede sustituir a b a puede sustituir a b |
Si x = 4 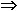 2(x) + 3 = 2(4) + 3 2(x) + 3 = 2(4) + 3 |
Propiedad aditiva de la igualdad:
Si sumamos el mismo número a ambos lados de la igualdad, la igualdad permanece |
Si a = b 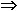 a + c = b + c a + c = b + c |
Si x = 4 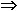 x + 2 = 4 + 2 x + 2 = 4 + 2 |
Propiedad multiplicativa de la igualdad:
Si multiplicamos el mismo número en ambos lados de la igualdad, la igualdad permanece |
Si a = b 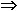 a . c = b . c a . c = b . c |
Si x = 4 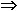 x . 2 = 4 . 2 x . 2 = 4 . 2 |
|
|
![]() R
R