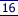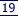[a + (-a)] = 0 |
Por el postulado del inverso aditivo
si a 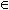 R R 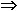 a + (-a) = 0 a + (-a) = 0 |
[a + (-a)] . b = 0 . b |
Por la propiedad multiplicativa de la igualdad. Podemos multiplicar el mismo número en ambos lados de la igualdad sin alterar la igualdad.
Si a, b, c 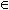 R y a = b R y a = b 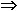 a . c = b . c a . c = b . c |
a . b + (-a) . b = 0 . b |
Por la propiedad distributiva:
Si a, b, c 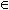 R R 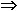 (a + b) . c = a . c + b . c (a + b) . c = a . c + b . c |
a . b + (-a) . b = 0 |
Por el teorema de la multiplicación por cero que acabamos de demostrar
Si x 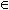 R R 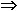 x . 0 = 0 x . 0 = 0 |
(a . b) + (-a) . b - (a . b) = 0 - (a . b) |
Por la propiedad aditiva de la igualdad, podemos sumar el mismo número en ambos lados de la igualdad sin alterar la igualdad
Si a, b, c 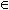 R y a = b R y a = b 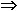 a + . c = b + . c a + . c = b + . c |
(a . b) + (-a) . b - (a . b) = - (a . b) |
Por el elemento identidad de la suma, Si a 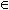 R R 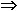 a + 0 = a a + 0 = a |
(a . b) - (a . b) + (-a) . b = - (a . b) |
Por la propiedad conmutativa para la suma
Si a, b 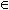 R R 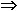 a + b = b + a a + b = b + a |
0 + (-a) . b = - (a . b) |
Por el inverso aditivo para la suma
Si a, b 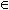 R R 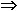 a + (-a) = 0 a + (-a) = 0 |
(-a) . b = - (a . b) |
Por el elemento identidad de la suma, Si a 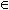 R R 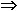 a + 0 = a a + 0 = a |
(-a) . b = - (a . b) |
Es lo que queríamos demostrar: el producto de dos factores con signos contrarios es negativo:
Si a y b 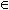 R R 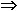 (-a) . b = -(a . b) (-a) . b = -(a . b) |
![]() R y por lo tanto se cumplen los postulados y propiedades conocidos.
R y por lo tanto se cumplen los postulados y propiedades conocidos.